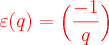La loi de réciprocité quadratique
Table des matières
On note, pour tout entier premier p,  .
.
On rappelle qu’il s’agit d’un corps à p éléments. D’autre part,  est
un groupe cyclique d’ordre p - 1.
est
un groupe cyclique d’ordre p - 1.
On dit qu’un élément  est un carré s’il existe
est un carré s’il existe  tel que
tel que
 .
.
Définition 1 Pour  et p un nombre premier supérieur ou égal à 3,
le symbole de Legendre
et p un nombre premier supérieur ou égal à 3,
le symbole de Legendre 

 est défini par :
est défini par :

On dispose alors le résultat suivant dû à Euler :
Proposition 2 Soit p un nombre premier ≥ 3. Il y a autant de carrés que de
non carrés dans  . Pour tout
. Pour tout  , on a la formule
, on a la formule
![(n-) p-1
p ≡ n 2 [p].](../../docs/cours/2/212x.png)
DEMONSTRATION : L’application  défini par
défini par  est
morphisme de groupe multiplicatif, dont le noyau est {-1, 1} (de cardinal 2 car
p ≥ 3) et dont l’image est l’ensemble
est
morphisme de groupe multiplicatif, dont le noyau est {-1, 1} (de cardinal 2 car
p ≥ 3) et dont l’image est l’ensemble  des carrés de
des carrés de  . Par un théorème
d’isomorphisme, il vient
. Par un théorème
d’isomorphisme, il vient 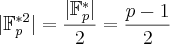 , ce qui prouve la première
assertion.
, ce qui prouve la première
assertion.
Pour tout  , le théorème de Fermat nous donne
, le théorème de Fermat nous donne  et donc
et donc
 . Chacune des équations
. Chacune des équations  a au plus
a au plus  racines
donc exactement
racines
donc exactement  racines.
racines.
Si  est un carré, on a
est un carré, on a  . Sinon, c’est que
. Sinon, c’est que
 . □
. □
On en déduit immédiatement le
Corollaire 1 Pour  et p premier ≥ 3,
et p premier ≥ 3,

Proposition 3 Soit q un nombre premier ≥ 3, soit A un anneau et soit
On définit la somme de Gauss
 tel que
tel que


DEMONSTRATION : Notons tout d’abord que  ; en effet,
; en effet,
 .
.
D’autre part, on calcule

 désigne
désigne  .
.
Si k=0 et i
 0, alors
0, alors  et on en déduit
et on en déduit
 .
.
Supposons k
 0. Alors en notant
0. Alors en notant  l’inverse de i dans
l’inverse de i dans  ,
,

Or, l’application  ,
,  étant clairement bijective, il
vient
étant clairement bijective, il
vient

la dernière inégalité étant une conséquence de la proposition 2.
On a donc trouvé

ce qui prouve la première partie de la proposition.
A étant de caractéristique p, l’application  de
de  dans lui-même est
un morphisme de corps, appelé morphisme de Frobenius. On peut donc
calculer
dans lui-même est
un morphisme de corps, appelé morphisme de Frobenius. On peut donc
calculer
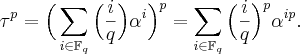
L’entier p étant impair,  et donc
et donc

On a utilisé le fait que, p étant inversible dans  , l’application
, l’application 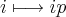 est
bijective. □
est
bijective. □
Voici le résultat principal de cet article.
Théorème 4 Soit p et q deux nombres premiers distincts ≥ 3. Alors

DEMONSTRATION : On se place dans l’anneau ![A = 𝔽p[X] ∕(Φq)](../../docs/cours/2/261x.png) où
où  est le
polynôme cyclotomique
est le
polynôme cyclotomique  . Dans cet anneau quotient de
caractéristique p, on note α la classe de X, de sorte que
. Dans cet anneau quotient de
caractéristique p, on note α la classe de X, de sorte que  . On
définit
. On
définit

D’après la proposition 2, on a 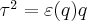 et donc
et donc  .
.
D’autre part toujours d’après cette proposition,  et on en
déduit
et on en
déduit

Puisque τ est inversible (car  l’est), c’est que
l’est), c’est que

comme annoncé. □


Nous sommes le Samedi 20 Avril 2024 et il est 02:12
 >
>